1829: Maximum XOR for Each Query - Optimized Solution
The problem "Maximum XOR for Each Query" (LeetCode 1829) requires us to find the maximum XOR result for each query on an array. Given a sorted array of non-negative integers and a maximumBit value, we need to determine the optimal k for each query that maximizes the XOR operation with the cumulative XOR of the array elements.
Problem Statement
You are given a sorted array of non-negative integers nums and an integer maximumBit.
You need to perform n queries (where n is the size of the array) where for each query:
- Compute the XOR of all elements in the array up to the current position
- Find a non-negative integer k (where 0 ≤ k < 2maximumBit) that maximizes the XOR result
- After each query, remove the last element from the array
Constraints
1 ≤ nums.length ≤ 1050 ≤ nums[i] ≤ 2maximumBit - 11 ≤ maximumBit ≤ 20
Problem Link
Example
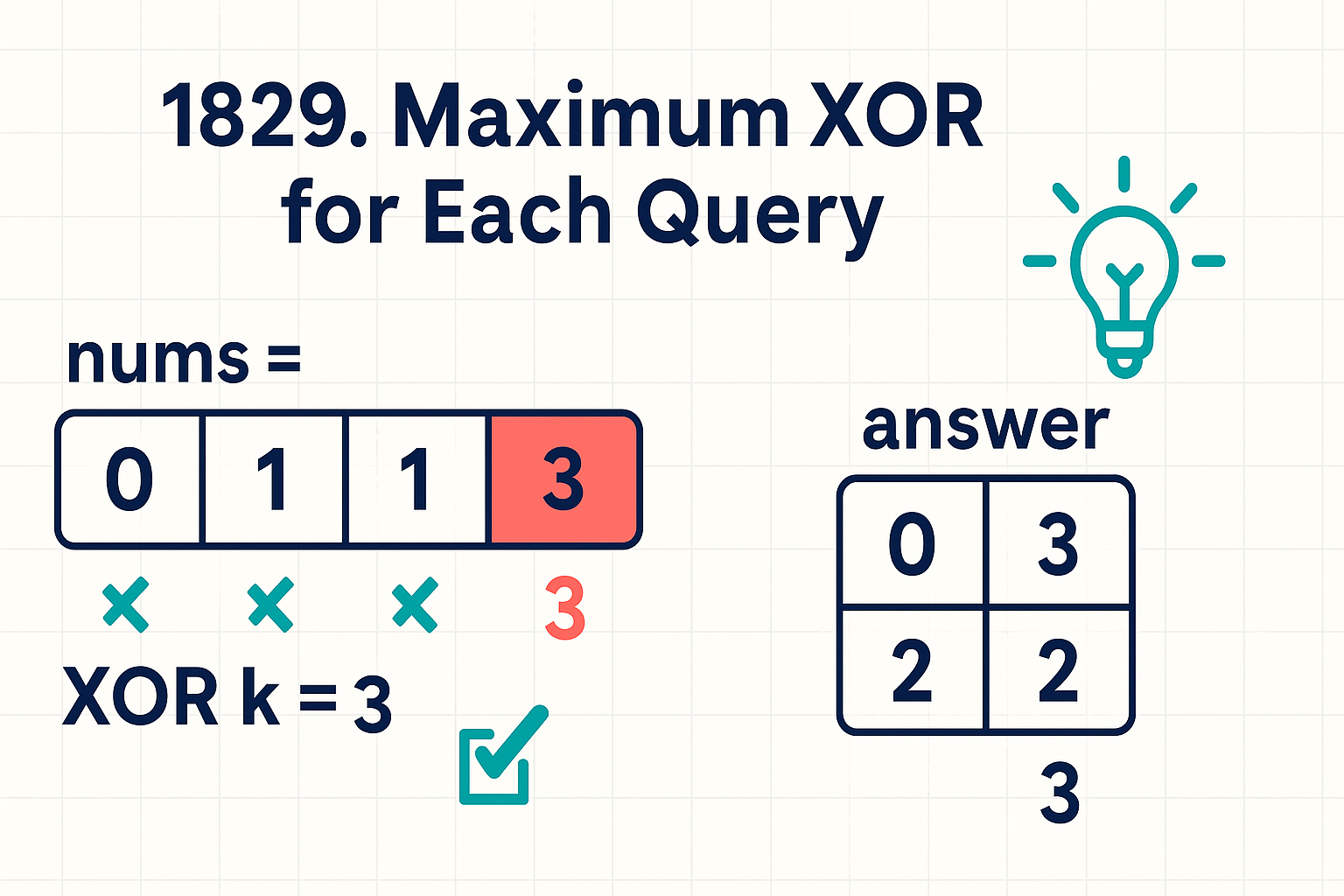
Input: nums = [0, 1, 1, 3], maximumBit = 2
Output: [0, 3, 2, 3]
Explanation:
Query 1: nums = [0,1,1,3], k = 0 → 0 XOR 1 XOR 1 XOR 3 XOR 0 = 3
Query 2: nums = [0,1,1], k = 3 → 0 XOR 1 XOR 1 XOR 3 = 3
Query 3: nums = [0,1], k = 2 → 0 XOR 1 XOR 2 = 3
Query 4: nums = [0], k = 3 → 0 XOR 3 = 3Approach 1: Brute Force (TLE)
The brute force approach checks every possible value of k for each query and calculates the XOR of all elements in the current array. While straightforward, this approach results in O(n² * 2maximumBit) time complexity, which is too slow for large inputs.
Algorithm Steps
- Initialize an empty result array
- Iterate through each query (from last element to first)
- For each query, compute the XOR of all elements in the current array
- Try all possible k values from 0 to 2maximumBit-1
- Find the k that maximizes the XOR result
- Add the best k to the result array
- Remove the last element from the array
Complexity Analysis
| Time Complexity | Space Complexity |
|---|---|
| O(n² * 2maximumBit) | O(n) |
Why it fails: For n = 105 and maximumBit = 20, the number of operations would be around 105 * 105 * 220 ≈ 1015, which is way beyond what's acceptable.
Implementation
class Solution {
public:
vector<int> getMaximumXor(vector<int>& nums, int maximumBit) {
int n = nums.size();
vector<int> ans(n);
int maxK = (1 << maximumBit) - 1;
for (int i = n - 1; i >= 0; --i) {
int currentXor = 0;
for (int j = 0; j <= i; ++j) {
currentXor ^= nums[j];
}
int bestK = 0;
for (int k = 0; k <= maxK; ++k) {
if ((currentXor ^ k) > (currentXor ^ bestK)) {
bestK = k;
}
}
ans[i] = bestK;
}
return ans;
}
};
class Solution {
public int[] getMaximumXor(int[] nums, int maximumBit) {
int n = nums.length;
int[] ans = new int[n];
int maxK = (1 << maximumBit) - 1;
for (int i = n - 1; i >= 0; i--) {
int currentXor = 0;
for (int j = 0; j <= i; j++) {
currentXor ^= nums[j];
}
int bestK = 0;
for (int k = 0; k <= maxK; k++) {
if ((currentXor ^ k) > (currentXor ^ bestK)) {
bestK = k;
}
}
ans[n - 1 - i] = bestK;
}
return ans;
}
}
class Solution:
def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:
n = len(nums)
ans = [0] * n
max_k = (1 << maximumBit) - 1
for i in range(n-1, -1, -1):
current_xor = 0
for j in range(i+1):
current_xor ^= nums[j]
best_k = 0
for k in range(max_k + 1):
if (current_xor ^ k) > (current_xor ^ best_k):
best_k = k
ans[n - 1 - i] = best_k
return ans
Approach 2: Cumulative XOR with Bit Manipulation (Optimal)
The optimal solution uses cumulative XOR and bit manipulation to find the maximum XOR result efficiently. By recognizing that the optimal k is always (1 << maximumBit) - 1 XOR cumulative_xor, we can avoid the nested loops of the brute force approach.
Key Insights
- The maximum possible XOR result is always (1 << maximumBit) - 1
- The optimal k is (max_value XOR cumulative_xor)
- We can compute cumulative XOR in reverse order to reuse previous computations
- No need to try all possible k values - we can calculate the optimal k directly
Algorithm Steps
- Compute the maximum possible value: (1 << maximumBit) - 1
- Initialize cumulative XOR to 0 and result array
- Iterate through the array in reverse order:
- Update cumulative XOR with current element
- Calculate optimal k as (max_value XOR cumulative_xor)
- Store k in result array
- Return the result array
Complexity Analysis
| Time Complexity | Space Complexity |
|---|---|
| O(n) | O(n) |
Explanation: We only traverse the array once, and each XOR operation is O(1). The space is O(n) for the result array.
Implementation
class Solution {
public:
vector<int> getMaximumXor(vector<int>& nums, int maximumBit) {
int n = nums.size();
int max_val = (1 << maximumBit) - 1;
vector<int> ans(n);
int cumulative_xor = 0;
for (int i = n - 1; i >= 0; i--) {
cumulative_xor ^= nums[n - 1 - i];
ans[i] = max_val ^ cumulative_xor;
}
return ans;
}
};
class Solution {
public int[] getMaximumXor(int[] nums, int maximumBit) {
int n = nums.length;
int max_val = (1 << maximumBit) - 1;
int[] ans = new int[n];
int cumulative_xor = 0;
for (int i = 0; i < n; i++) {
cumulative_xor ^= nums[n - 1 - i];
ans[i] = max_val ^ cumulative_xor;
}
return ans;
}
}
class Solution:
def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:
n = len(nums)
max_val = (1 << maximumBit) - 1
ans = [0] * n
cumulative_xor = 0
for i in range(n):
cumulative_xor ^= nums[n - 1 - i]
ans[i] = max_val ^ cumulative_xor
return ans
Approach 3: Prefix XOR (Alternative Optimal Solution)
This alternative solution computes the prefix XOR array first, then calculates the optimal k for each query. It's slightly different in implementation but has the same time complexity.
Implementation
class Solution {
public:
vector<int> getMaximumXor(vector<int>& nums, int maximumBit) {
int n = nums.size();
int max_val = (1 << maximumBit) - 1;
vector<int> prefix(n + 1, 0);
vector<int> ans(n);
// Compute prefix XOR
for (int i = 0; i < n; i++) {
prefix[i + 1] = prefix[i] ^ nums[i];
}
// Compute answers in reverse
for (int i = 0; i < n; i++) {
ans[i] = max_val ^ prefix[n - i];
}
return ans;
}
};
class Solution {
public int[] getMaximumXor(int[] nums, int maximumBit) {
int n = nums.length;
int max_val = (1 << maximumBit) - 1;
int[] prefix = new int[n + 1];
int[] ans = new int[n];
// Compute prefix XOR
for (int i = 0; i < n; i++) {
prefix[i + 1] = prefix[i] ^ nums[i];
}
// Compute answers in reverse
for (int i = 0; i < n; i++) {
ans[i] = max_val ^ prefix[n - i];
}
return ans;
}
}
class Solution:
def getMaximumXor(self, nums: List[int], maximumBit: int) -> List[int]:
n = len(nums)
max_val = (1 << maximumBit) - 1
prefix = [0] * (n + 1)
ans = [0] * n
# Compute prefix XOR
for i in range(n):
prefix[i + 1] = prefix[i] ^ nums[i]
# Compute answers in reverse
for i in range(n):
ans[i] = max_val ^ prefix[n - i]
return ans
Edge Cases and Special Considerations
When implementing solutions for this problem, consider these edge cases:
1. Single Element Array
Input: nums = [5], maximumBit = 3
Output: [2]
Explanation: max_val = 7 (2^3-1), k = 7 XOR 5 = 22. All Elements Zero
Input: nums = [0, 0, 0], maximumBit = 2
Output: [3, 3, 3]
Explanation: XOR is always 0, so k is always 3 (2^2-1)3. Maximum Bit Value
Input: nums = [1, 2, 3], maximumBit = 1
Output: [0, 1, 1]
Explanation: max_val = 1 (2^1-1), so k can only be 0 or 14. Large Input Size
Input: nums = [1, 2, 3, ..., 100000], maximumBit = 20
Output: Array of 100000 elements
Must handle efficiently with O(n) solutionComparison of Approaches
| Approach | Time Complexity | Space Complexity | When to Use | Pros | Cons |
|---|---|---|---|---|---|
| Brute Force | O(n² * 2maximumBit) | O(n) | Small inputs only | Simple to understand | Fails for large n |
| Cumulative XOR | O(n) | O(n) | All cases, optimal | Most efficient | Requires bit manipulation insight |
| Prefix XOR | O(n) | O(n) | When prefix array is useful | Clear separation of steps | Uses extra space |
Frequently Asked Questions
1. Why does XOR with (1 << maximumBit) - 1 give the maximum result?
(1 << maximumBit) - 1 creates a number with all bits set to 1 within the maximumBit range. XOR-ing with this value flips all bits of the original number, giving the maximum possible value in that bit range.
2. How does the cumulative XOR approach work in reverse?
By processing the array in reverse, we can build the cumulative XOR for each query efficiently. The XOR for nums[0..i] is the same as XOR(nums[0..n-1]) XOR XOR(nums[i+1..n-1]). This allows us to compute each query's XOR in constant time.
3. Can this problem be solved without bit manipulation?
While possible, it would be much less efficient. Bit manipulation allows us to compute the optimal k directly without trying all possibilities. Other approaches would likely result in higher time complexity.
4. What if the array wasn't sorted?
The solution doesn't depend on the array being sorted. The order of XOR operations doesn't matter (XOR is commutative and associative), so the approach works regardless of the array's order.
5. How would you modify the solution if we needed to keep the array intact?
You could make a copy of the array or use indices to track the current subarray without modifying the original array. The time and space complexity would remain the same.
6. Is the prefix XOR approach better than the cumulative XOR approach?
Both have O(n) time complexity. The prefix XOR approach uses slightly more space (O(n) vs O(1)) but may be more intuitive for some. The cumulative XOR approach is more space-efficient.
7. How does this problem relate to real-world applications?
XOR operations are fundamental in cryptography, error detection, and data compression. This problem demonstrates how to maximize XOR results efficiently, which is useful in encryption algorithms and checksum calculations.
8. What similar problems should I practice to master this pattern?
Recommended problems: 421 (Maximum XOR of Two Numbers in an Array), 1318 (Minimum Flips to Make a OR b Equal to c), 1442 (Count Triplets That Can Form Two Arrays of Equal XOR), and 1734 (Decode XORed Permutation).