1920: Build Array from Permutation

Difficulty: Easy

Topics: Arrays, In-place Algorithms

Companies: Amazon, Google, Microsoft

Pro Tip: The optimal solution requires understanding of modular arithmetic for in-place array transformations. Focus on encoding two values in one position.

Problem Statement

Given a zero-based permutation array nums, return an array ans where ans[i] = nums[nums[i]] for each index i. Solve it with O(1) extra space for bonus points.

Example 1

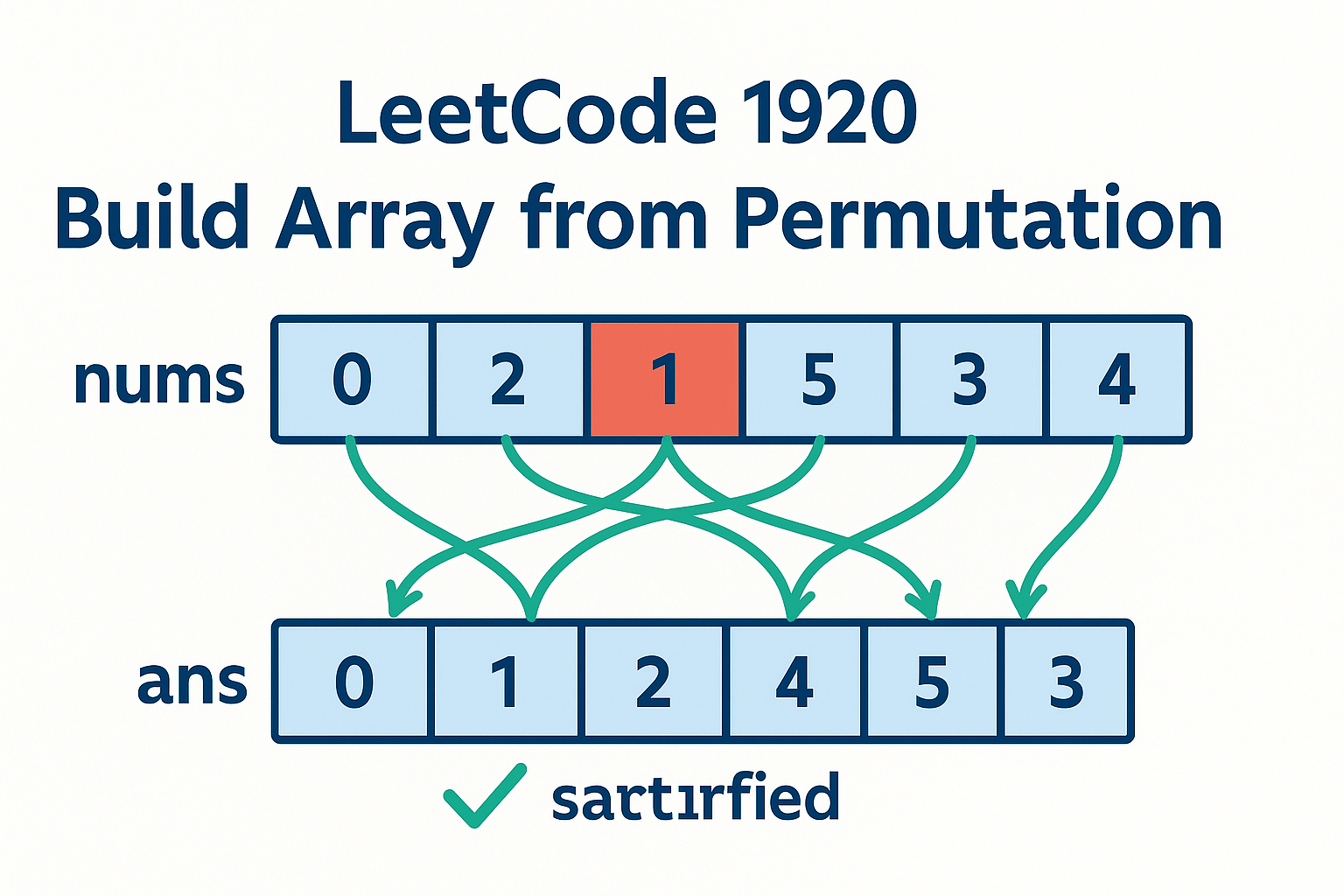
Input: nums = [0,2,1,5,3,4]
Output: [0,1,2,4,5,3]
Explanation: Each element is nums[nums[i]]

Example 2

Input: nums = [5,0,1,2,3,4]
Output: [4,5,0,1,2,3]
Explanation: Transformation done in-place

Problem Link: View on LeetCode ↗

Approach 1: Straightforward Solution (O(n) Space)

Create a new array and fill it with transformed values.

Algorithm Steps

Initialize empty result array
Iterate through each index
Store nums[nums[i]] in result

Complexity Analysis

Time Complexity	Space Complexity
O(n)	O(n)

Basic Solution

class Solution {
public:
    vector<int> buildArray(vector<int>& nums) {
        vector<int> ans(nums.size());
        for(int i = 0; i < nums.size(); ++i) {
            ans[i] = nums[nums[i]];
        }
        return ans;
    }
};

class Solution {
    public int[] buildArray(int[] nums) {
        int[] ans = new int[nums.length];
        for(int i = 0; i < nums.length; i++) {
            ans[i] = nums[nums[i]];
        }
        return ans;
    }
}

class Solution:
    def buildArray(self, nums: List[int]) -> List[int]:
        return [nums[num] for num in nums]

Implementation Note: This simple approach is optimal when O(n) space is acceptable. Preferred for readability in most cases.

Approach 2: In-place O(1) Space Solution

Encode two values in each position using mathematical manipulation.

Algorithm Steps

Use formula: nums[i] += n * (nums[nums[i]] % n)
Divide each element by n to get final values
Modulo operation preserves original value

Complexity Analysis

Time Complexity	Space Complexity
O(n)	O(1)

In-place Solution

class Solution {
public:
    vector<int> buildArray(vector<int>& nums) {
        int n = nums.size();
        for(int i = 0; i < n; ++i) {
            nums[i] += n * (nums[nums[i]] % n);
        }
        for(int i = 0; i < n; ++i) {
            nums[i] /= n;
        }
        return nums;
    }
};

class Solution {
    public int[] buildArray(int[] nums) {
        int n = nums.length;
        for(int i = 0; i < n; i++) {
            nums[i] += n * (nums[nums[i]] % n);
        }
        for(int i = 0; i < n; i++) {
            nums[i] /= n;
        }
        return nums;
    }
}

class Solution:
    def buildArray(self, nums: List[int]) -> List[int]:
        n = len(nums)
        for i in range(n):
            nums[i] += n * (nums[nums[i]] % n)
        for i in range(n):
            nums[i] //= n
        return nums

Implementation Note: This advanced technique encodes both original and new values using mathematical operations. The modulo preserves original values during overwriting.

Approach Comparison

Approach	Time	Space	Use Case
Basic Solution	O(n)	O(n)	Readability, Small input
In-place Solution	O(n)	O(1)	Large datasets, Memory constraints

Important: The in-place method modifies the input array. Use defensive copying if original array must be preserved.

Edge Cases and Testing

1. Minimum Input (n=1)

Input: [0] → Output: [0]

2. Maximum Permutation

Input: [4,3,2,1,0] → Output: [0,1,2,3,4]

3. Cyclic Dependencies

Input: [2,0,1] → Output: [1,2,0]

Warning: Always test for self-referential indices where nums[i] = i

Frequently Asked Questions

1. Why does the in-place method work with modulo?

Using nums[nums[i]] % n preserves the original value before any modifications during the first pass, ensuring correct calculations.

2. How does encoding two values work?

We store new_value * n + original_value in each position. Division by n extracts new value, modulo gets original (but not needed in final result).

3. What if nums contains large numbers?

The problem constraints guarantee 0 ≤ nums[i] < n, making the encoding safe within standard integer ranges.

4. Why multiply by n instead of other numbers?

Since all values are < n, multiplying by n creates a unique base-n encoding that prevents information overlap.

5. Can we solve this with bit manipulation?

Yes, but modulo/division approach is more readable. Bitwise methods would need sufficient bit space (unlikely in practice).

6. How to handle overflow?

Constraints ensure n ≤ 1000, so 1000*1000 = 1,000,000 fits in 32-bit integers (max 2,147,483,647).

7. Does order of processing matter?

Yes! Must complete first full pass before starting division pass to prevent data corruption.

8. What if nums is read-only?

Use basic O(n) space approach. The in-place solution requires write access.

9. How to verify correctness?

Check ans[i] = nums[nums[i]] for all i. Test with cyclic permutations and edge cases.

10. Why is this problem important?

Teaches advanced array manipulation techniques crucial for memory-constrained environments and low-level programming.

Final Insight: This problem beautifully demonstrates how mathematical number theory can optimize space complexity in array transformations. The in-place solution is a perfect example of thinking "outside the box" while respecting constraints.