3618: Split Array by Prime Indices
Problem Statement
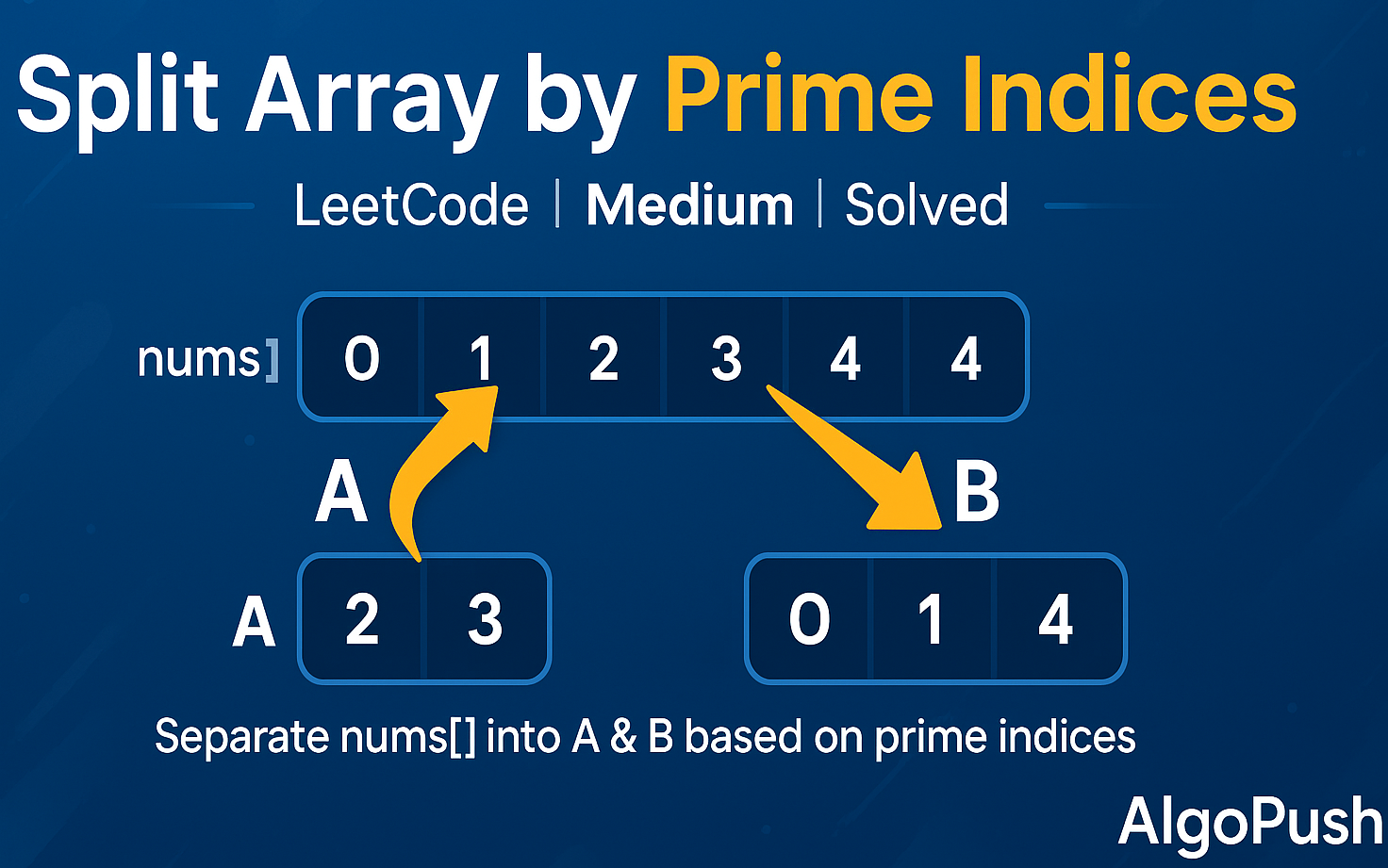
Given an integer array nums, split it into two arrays A and B following these rules:
- Elements at prime indices go into array A
- All other elements go into array B
Return the absolute difference between the sums of the two arrays: |sum(A) - sum(B)|.
Note: Prime numbers are natural numbers greater than 1 with exactly two distinct factors: 1 and themselves. An empty array has a sum of 0.
Example 1
Input: nums = [2, 3, 4]
Prime Indices: 2 (since index 2 is prime)
Array A: [4]
Array B: [2, 3]
Output: |4 - (2+3)| = |4-5| = 1
Example 2
Input: nums = [-1, 5, 7, 0]
Prime Indices: 2, 3
Array A: [7, 0]
Array B: [-1, 5]
Output: |(7+0) - (-1+5)| = |7 - 4| = 3
Approach 1: Brute-force Prime Checking
Check each index for primality using trial division, then calculate the sums.
Algorithm Steps
- Initialize two sums: sumA (for prime indices) and sumB (for non-prime indices)
- Iterate through each index i in the array
- For each index, check if it's prime using a helper function
- If prime, add nums[i] to sumA
- Otherwise, add nums[i] to sumB
- Return |sumA - sumB|
Complexity Analysis
| Time Complexity | Space Complexity |
|---|---|
| O(n√n) | O(1) |
class Solution {
public:
bool isPrime(int n) {
if (n <= 1) return false;
for (int i = 2; i * i <= n; i++) {
if (n % i == 0)
return false;
}
return true;
}
long long splitArray(vector<int>& nums) {
long long sumA = 0, sumB = 0;
int n = nums.size();
for (int i = 0; i < n; i++) {
if (isPrime(i)) {
sumA += nums[i];
} else {
sumB += nums[i];
}
}
return abs(sumA - sumB);
}
};class Solution {
private boolean isPrime(int n) {
if (n <= 1) return false;
for (int i = 2; i * i <= n; i++) {
if (n % i == 0)
return false;
}
return true;
}
public long splitArray(int[] nums) {
long sumA = 0, sumB = 0;
int n = nums.length;
for (int i = 0; i < n; i++) {
if (isPrime(i)) {
sumA += nums[i];
} else {
sumB += nums[i];
}
}
return Math.abs(sumA - sumB);
}
}class Solution:
def isPrime(self, n: int) -> bool:
if n <= 1:
return False
i = 2
while i * i <= n:
if n % i == 0:
return False
i += 1
return True
def splitArray(self, nums: List[int]) -> int:
sumA, sumB = 0, 0
n = len(nums)
for i in range(n):
if self.isPrime(i):
sumA += nums[i]
else:
sumB += nums[i]
return abs(sumA - sumB)Approach 2: Optimized with Sieve of Eratosthenes
Precompute prime indices using the Sieve algorithm for O(1) prime checks during iteration.
Algorithm Steps
- Create a boolean array
isPrimeof size n (array length) - Initialize all elements as true (assuming all are prime initially)
- Mark 0 and 1 as non-prime (since primes start from 2)
- Iterate from 2 to √n: if current number is prime, mark all its multiples as non-prime
- Iterate through the array: if
isPrime[i]is true, add to sumA; else add to sumB - Return |sumA - sumB|
Complexity Analysis
| Time Complexity | Space Complexity |
|---|---|
| O(n log log n) | O(n) |
class Solution {
public:
long long splitArray(vector<int>& nums) {
int n = nums.size();
if (n == 0) return 0;
// Create sieve array
vector<bool> isPrime(n, true);
if (n > 0) isPrime[0] = false; // index 0 is not prime
if (n > 1) isPrime[1] = false; // index 1 is not prime
// Sieve of Eratosthenes
for (int i = 2; i * i < n; i++) {
if (isPrime[i]) {
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
}
long long sumA = 0, sumB = 0;
for (int i = 0; i < n; i++) {
if (isPrime[i]) {
sumA += nums[i];
} else {
sumB += nums[i];
}
}
return abs(sumA - sumB);
}
};class Solution {
public long splitArray(int[] nums) {
int n = nums.length;
if (n == 0) return 0;
// Create sieve array
boolean[] isPrime = new boolean[n];
Arrays.fill(isPrime, true);
if (n > 0) isPrime[0] = false;
if (n > 1) isPrime[1] = false;
// Sieve of Eratosthenes
for (int i = 2; i * i < n; i++) {
if (isPrime[i]) {
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
}
long sumA = 0, sumB = 0;
for (int i = 0; i < n; i++) {
if (isPrime[i]) {
sumA += nums[i];
} else {
sumB += nums[i];
}
}
return Math.abs(sumA - sumB);
}
}class Solution:
def splitArray(self, nums: List[int]) -> int:
n = len(nums)
if n == 0:
return 0
# Create sieve array
is_prime = [True] * n
if n > 0:
is_prime[0] = False
if n > 1:
is_prime[1] = False
# Sieve of Eratosthenes
i = 2
while i * i < n:
if is_prime[i]:
j = i * i
while j < n:
is_prime[j] = False
j += i
i += 1
sumA, sumB = 0, 0
for i in range(n):
if is_prime[i]:
sumA += nums[i]
else:
sumB += nums[i]
return abs(sumA - sumB)Approach 3: Single Pass with Precomputed Primes
Precompute primes up to maximum possible n (10^5) once for efficiency in repeated calls.
Algorithm Steps
- Precompute primes up to 100000 (max constraint) using Sieve of Eratosthenes
- Store results in a global boolean array
- For each input array, simply iterate through indices
- Check if index is prime using precomputed array
- Calculate sums and return the absolute difference
Complexity Analysis
| Time Complexity | Space Complexity |
|---|---|
| O(n) per call | O(max_n) |
class Solution {
private:
vector<bool> primes;
bool computed = false;
void computePrimes(int max_n) {
primes = vector<bool>(max_n + 1, true);
if (max_n >= 0) primes[0] = false;
if (max_n >= 1) primes[1] = false;
for (int i = 2; i * i <= max_n; i++) {
if (primes[i]) {
for (int j = i * i; j <= max_n; j += i) {
primes[j] = false;
}
}
}
computed = true;
}
public:
long long splitArray(vector<int>& nums) {
int n = nums.size();
if (!computed || n >= primes.size()) {
computePrimes(100000); // max constraint
}
long long sumA = 0, sumB = 0;
for (int i = 0; i < n; i++) {
if (primes[i]) {
sumA += nums[i];
} else {
sumB += nums[i];
}
}
return abs(sumA - sumB);
}
};Approach Comparison
| Approach | Time Complexity | Space Complexity | Best For |
|---|---|---|---|
| Brute-force | O(n√n) | O(1) | Small inputs (n < 1000) |
| Sieve of Eratosthenes | O(n log log n) | O(n) | Large inputs (n ≤ 10^5) |
| Precomputed Primes | O(n) per call | O(max_n) | Repeated function calls |
Edge Cases and Testing
1. Empty Array
Input: [] → Output: 02. Single Element Array
Input: [5] → Output: |0 - 5| = 5 (since index 0 is not prime)3. All Prime Indices
Input: [1, 2, 3, 4] (indices 2 and 3 are prime)
Output: |(3+4) - (1+2)| = |7 - 3| = 44. Negative Numbers
Input: [-1, -2, -3, -4]
Prime indices: 2,3 → sumA = -3 + -4 = -7
sumB = -1 + -2 = -3
Output: |-7 - (-3)| = |-4| = 4Frequently Asked Questions
1. Why is index 0 not considered prime?
Prime numbers are defined as natural numbers greater than 1 with exactly two distinct factors. Since 0 doesn't meet these criteria (it's not greater than 1), it's not prime.
2. How does the Sieve of Eratosthenes work?
The algorithm works by iteratively marking the multiples of each prime starting from 2. All remaining unmarked numbers are primes. It efficiently eliminates non-primes in O(n log log n) time.
3. Why start marking multiples from i*i?
When processing prime number i, all multiples smaller than i*i have already been marked by smaller primes. Starting from i*i optimizes the algorithm.
4. How to handle negative numbers?
Negative numbers are handled the same as positive numbers. Simply add them to the appropriate sum based on their index primality.
5. Can we solve this without extra space?
For large n (≤10^5), the brute-force approach uses O(1) space but is too slow. The Sieve approach requires O(n) space but is much faster.
6. Why use long for sums?
With n ≤ 10^5 and nums[i] up to 10^9, the total sum could be as large as 10^14, which exceeds 32-bit integer range. Using long prevents overflow.
7. Is 1 considered a prime number?
No, 1 is not a prime number. By definition, primes must have exactly two distinct positive divisors, and 1 has only one divisor (itself).
8. How to handle large inputs efficiently?
Always use the Sieve of Eratosthenes approach for large inputs. The brute-force method becomes impractical for n > 10,000.
9. Can we optimize further?
We can combine the prime marking and summing into a single loop, but the Sieve still dominates the time complexity. The current optimizations are sufficient for constraints.
10. Why absolute difference?
The problem asks for the absolute difference |sumA - sumB| to ensure a non-negative result regardless of which sum is larger.